Bola merupakan bangun tiga dimensi dengan pembatas berupa sisi-sisi berbentuk lengkung. Salah satu sifat bangun bola adalah sisi pembatasnya yang tidak terbatas jumlahnya. Untuk itu dalam bola terdapat volume yang berupa isi atau kapasitas yang terkandung dalam bola itu sendiri.
Sedangkan luas permukaan pada bola ialah area kulit berbentuk lingkaran yang membungkus bolanya. Bagaimana jika bola tersebut di potong menjadi dua? Bagaimana rumus luas permukaan setengah bola? Bagaimana rumus luas setengah bola pejal? Bagaimana cara menyelesaikan contoh soal setengah bola?
Temukan informasi dan latihan lebih banyak pada materi berikut ini!
Salam Cerdas dan Sehat!
Kembali lagi sobat solusi menyapa insan cerdas yang bernalar kristis dan semangat! Semoga semua dalam keadaan sehat, percaya diri, dan berkarakter jujur.
Literasi dapat menumbuhkembangkan karakter dan pola pikir. Melakukan kegiatan ini sebelum pembelajaran dimulai sangatlah bagus dan dianjurkan. Kegiatan literasi ini cukup dilakukan 10-15 menit secara rutin setiap hari. Kegiatan ini selain menambah pengetahuan dan wawasan diri, juga menumbuhkan budaya membaca dan menulis, serta menumbuhkembangkan budi pekerti agar menjadi pembelajar sepanjang hayat. Membaca cerita fiksi dan informasi, motivasi, artikel, solusi, cerita bergambar, menulis pengalaman diri atau kegiatan lainnya yang positif merupakan contoh kegiatan literasi yang dapat dilakukan.
Sebelum pembelajaran daring dimulai, ingat dan budayakan terlebih dahulu melakukan kegiatan sembahyang (berdoa memohon keselamatan diri, keluarga dan alam sekitar), melakukan aksi kebersihan lingkungan rumah serta melakukan Pola Hidup Bersih dan Sehat (PHBS).
Topik Pembelajaran kali ini membahas Mata Pelajaran Matematika Tentang Luas Permukaan Bangun Ruang Bola untuk kelas 6 SD, dengan penguasaan kompetensi dasar (KD). 3.4 Menjelaskan bangun ruang kubus, balok, prisma, limas, tabung, kerucut, dan bola serta bangun ruang gabungannya serta luas permukaan dan volume bangun ruang kubus dan balok.
Tujuan Pembelajaran
Dengan membaca bahan ajar, berdiskusi, dan menggali informasi di berbagai sumber, peserta didik dapat memahami materi ajar dan mengembangkan kompetensi diri dalam penerapan kehidupan sehari-hari dengan tepat
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
Untuk lebih jelasnya simak dan pahami materi ajar berikut ini!
Selain membaca bahan ajar di blog ini, kalian juga bisa membaca di buku paket matematika dan menggali informasi dari berbagai sumber.
Luas Permukaan Bangun Ruang Bola
Baca juga materi tentang:
(Baca disini) Materi bahan ajar matematika tentang pengertian, ciri dan sifat, jaring-jaring, dan menentukan luas permukaan bola
Rumus Setengah Bola (Luas Permukaan dan Volume)
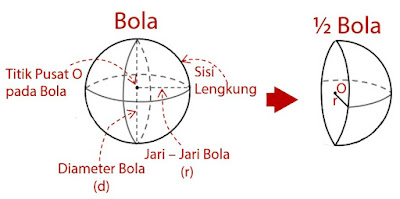
Dalam materi bola, kalian akan menjumpai dua rumus hitung yang berlaku. Pertama rumus luas permukaan dan yang kedua adalah rumus volume. Untuk rumus setengah bola sendiri cukup mudah yaitu hanya dengan membagi rumus volume dan luas permukaannya menjadi dua. Lalu bagaimana bentuk persamaan rumus luas permukaan setengah bola itu? Bagaimana persamaan rumus volume setengah bola itu? Meski rumusnya sederhana, namun bagaimana jika setengah bola tersebut pejal? Bagaimana rumus luas setengah bola pejal? Dalam bola pejal tersebut terdapat satu titik tengah, dimana semua sisinya mempunyai jarak yang sama. Titik ini dinamakan dengan titik pusat bola. Sedangkan jarak antara sisi lengkung dengan titik pusat bola dinamakan dengan jari jari bola.
Dalam bola itu juga terkandung diameter di dalamnya. Diameter sendiri merupakan jarak antara satu titik terjauh antara sisi lengkung dengan titik lainnya. Apabila di tengah bola utuh tepat dibagi menjadi dua, maka akan menghasilkan setengah bola yang sama besar. Maka dari itu rumus luas permukaan setengah bola dan rumus volume setengah bola berkaitan dengan rumus bola secara umum. Pada kesempatan kali ini saya akan menjelaskan tentang rumus setengah bola beserta contoh soal setengah bola. Untuk lebih jelasnya dapat anda simak di bawah ini.
Rumus Setengah Bola (Luas Permukaan dan Volume) Beserta Contoh Soal
Pada dasarnya rumus luas setengah bola merupakan luas permukaan bola yang utuh dibagi menjadi dua. Hal ini juga berlaku untuk volume bola. Maka dari itu sebelum anda memahami rumus luas setengah bola ini, alangkah lebih baik jika anda mengetahui terlebih dahulu mengenai rumus luas bola secara umum.
Luas permukaan pada dasarnya memiliki daerah yang berupa semua bagian yang membuat lingkaran menjadi tertutup. Secara umum luas permukaan bola dapat dirumuskan seperti di bawah ini:
Rumus Luas Permukaan Bola = 4πr²
Rumus di atas dapat digunakan untuk mengetahui luas permukaan setengah bola. Untuk rumus luas setengah bola sendiri dapat dibagi menjadi dua kategori yaitu rumus pada setengah bola pejal (bola padat) dan setengah bola berongga (bola tidak padat). Adapun rumus setengah bola untuk menghitung luas permukaannya yaitu:
Rumus Luas Permukaan Setengah Bola Berongga = 2πr²
Rumus Luas Permukaan Setengah Bola Pejal = 3πr²
Volume Setengah Bola
Setelah membagikan rumus luas setengah bola pejal dan berongga di atas. Selanjutnya saya akan menjelaskan tentang rumus volume setengah bola. Secara umum volume dapat diartikan sebagai isi atau kapasitan yang terkandung dalam bangun ruang. Hal ini juga berlaku untuk bangun ruang bola meskipun bentuknya hanya setengah. Setengah bola tersebut memiliki rumus volume yang berasal dari suatu percobaan. Pelaksanaan percobaan ini menggunakan bangun ruang bola dan kerucut. Kemudian tinggi kerucutnya memiliki nilai yang sama dengan jari jari bola dan jari jari alas kerucut. Untuk itu volume setengah bola dapat dirumuskan seperti di bawah ini:
Volume Bola Utuh = 4/3 πr³
Volume Setengah Bola = 2/3 πr³
Contoh soal
1. Perhatikan gambar di bawah ini!

Gambar di atas merupakan bangun ruang setengah bola pejal. Tentukan luas permukaan dan volumenya:
Pembahasan.
Contoh soal setengah bola pejal tersebut dapat diselesaikan dengan rumus seperti berikut:
Luas Permukaan Setengah Bola Pejal = 3πr²
Luas Permukaan Setengah Bola Pejal = 3 x 22/7 x 14 x 14
Luas Permukaan Setengah Bola Pejal = 1848 cm²
Volume Setengah Bola = 2/3 πr³
Volume Setengah Bola = 2/3 x 22/7 x 14 x 14
Volume Setengah Bola = 410,67 cm³
Jadi luas permukaan setengah bola pejal dan volume setengah bola ialah 1.848 cm² dan 410,67 cm³.
2. Setengah bola padat berbahan besi memiliki diameter 56 cm. Berapakah luas permukaanya?
Pembahasannya
Diketahui jari-jari adalah 56 cm.
Luas permukaan setengah bola padat yaitu luas bidang datar + luas bidang lengkung setengah bola.
Luas bidang datar = Luas lingkaran = π.r²
= (1/2) x (4.π.r²) = 2.π.r²
Maka, Luas permukaan sama dengan luas bidang datar + luas bidang lengkung
= π.r² + 2.π.r²
= 3.π.r²
= 3.(22/7).(56 cm)² = 3.(22/7).(56 cm × 56 cm)
= 29.568 cm²
Maka, luas permukaan setengah bola padat yaitu 29.568 cm².
Kolaborasi dan Praktik Baik
Kerjakan pertanyaan berikut untuk meningkatkan keterampilan dan mengembangkan kompetensi numerasimu dalam penerapan kehidupan sehari-hari (Kerjakan di buku latihanmu dengan menyertai tanda tangan orang tua!)
1. Sebuah bola memili ukuran luas permukaan 1.256 cm². Jika saat mengukur luas bola tersebut menggunakan nilai π = 3,14, Tentukan panjang diameter bola tersebut!
2. Perhatikan bangun setengah bola pejal berikut!

Tentukan luas permukaan bangun tersebut!
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
Bagaimana kegiatanya, menyenangkan bukan? Pekerjaan kalian yang sudah bagus dan luar biasa akan jauh lebih bermanfaat jika dilakukan presentasi atau di diskusikan dengan teman, orang tua, dan guru kalian. Hal ini bertujuan untuk meningkatkan rasa percaya diri dan membangun pengetahuan baru.
Hasil diskusi dan presentasi yang sudah kalian lakukan dapat dijadikan sebagai motivasi diri untuk perbaikan pembelajaran yang akan datang. Masukan atau saran juga kritik yang membangun dapat membangun karakter dan pengetahuan diri yang lebih baik.
Nah, untuk mengetahui pemahaman pembelajaran yang sudah kalian simak dan lakukan, ada baiknya juga kalian melakukan refleksi atau merangkum kegiatan pembelajaran hari ini. Hal tersebut bertujuan untuk menguji pemahaman kompetensi diri terhadap pembelajaran daring yang kalian lakukan secara mandiri dari rumah. Refleksi ini dapat dilakukan dengan menjawab pertanyaan singkat. Seperti :
Apa yang sudah saya pelajari hari ini?
Dapatkah saya menguasai materi pembelajaran hari ini?
Apa Manfaat yang saya dapatkan dengan mempelajari materi tersebut?
Demikian tayangan materi singkat Pembelajaran Jarak Jauh Matematika Tentang Luas Permukaan Bangun Ruang Bola untuk Kelas 6 SD. Untuk menguji pemahaman dan penguasaan kompetensi pembelajaran hari ini, lakukanlah kegiatan formatif berikut ini dengan menjawab soal yang terdiri dari 10 butir soal pilihan ganda dalam bentuk aplikasi google form.
Baca dan ikuti petunjuk soal yang disediakan. Jawab soal berikut dengan cermat agar bisa mengukur capaian kompetensi yang dimiliki.
Waktu pengerjaan dari Liang Solusi: 120:00 Menit!
Klik Saja untuk kalian yang ingin mengembangkan kompetensi melalui materi, penugasan dan penilaian soal formatif pada setiap pembelajaran
Setelah menyelesaikan soal tersebut, lihatlah skor perolehan kalian dan skor perolehan teman-teman kalian dari sekolah maupun antar sekolah pada form berikut ini!
Terima kasih sudah menyimak materi dan mengerjakan Pembelajaran Matematika Tentang Luas Permukaan Bangun Ruang Bola untuk Kelas 6 SD. Isi postingan ini tentu belum lengkap dan memberikan pembelajaran bermakna.
Untuk itu, kritik dan saran sangat dibutuhkan untuk meningkatkan kualitas situs www.liangsolusi.com ini. Semoga materi dan evaluasi formatif yang dilakukan bermanfaat untuk kalian. Salam solusi!
Kami sangat berterima kasih jika pembelajar berkenan membagikan postingan ini di media sosial! Budayakan meninggalkan komentar dan sebarkan jika bermanfaat setelah mengerjakannya. Semoga bertambah cerdas dan berkarakter.
#MerdekaBelajar
#CerdasBerkarakter
#Belajardarimanasaja












0 comments:
Posting Komentar