Ayo, masih ingat tentang prisma dan tabung pada materi sebelumnya? Ups... kalian tu memang hebat dan cermat ya!
Prisma merupakan salah satu bangun ruang tiga dimensi yang dibatasi oleh alas dan tutup dimana keduanya identik dengan bentuk tertentu, misal segitiga, segiempat, dan sebagainya.
Tabung atau silinder merupakan salah satu bangun ruang tiga dimensi yang dibentuk oleh 2 lingkaran identitik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut.
Namun bagaimana jika cara menentukan luas permukaan bangun prisma dan tabung? mulai penasaran nie sahabat solusi? yuk geser layar kalian ke bawah ya!!!
Salam Cerdas dan Sehat!
Kembali lagi sobat solusi menyapa insan cerdas yang bernalar kristis dan semangat! Semoga semua dalam keadaan sehat, percaya diri, dan berkarakter jujur.
Literasi dapat menumbuhkembangkan karakter dan pola pikir. Melakukan kegiatan ini sebelum pembelajaran dimulai sangatlah bagus dan dianjurkan. Kegiatan literasi ini cukup dilakukan 10-15 menit secara rutin setiap hari. Kegiatan ini selain menambah pengetahuan dan wawasan diri, juga menumbuhkan budaya membaca dan menulis, serta menumbuhkembangkan budi pekerti agar menjadi pembelajar sepanjang hayat. Membaca cerita fiksi dan informasi, motivasi, artikel, solusi, cerita bergambar, menulis pengalaman diri atau kegiatan lainnya yang positif merupakan contoh kegiatan literasi yang dapat dilakukan.
Sebelum pembelajaran daring dimulai, ingat dan budayakan terlebih dahulu melakukan kegiatan sembahyang (berdoa memohon keselamatan diri, keluarga dan alam sekitar), melakukan aksi kebersihan lingkungan rumah serta melakukan Pola Hidup Bersih dan Sehat (PHBS).
Topik Pembelajaran kali ini membahas Mata Pelajaran Matematika Tentang Luas Permukaan Prisma dan Tabung untuk kelas 6 SD, dengan penguasaan kompetensi dasar (KD). 3.4 Menjelaskan bangun ruang kubus, balok, prisma, limas, tabung, kerucut, dan bola serta bangun ruang gabungannya serta luas permukaan dan volume bangun ruang kubus dan balok.
Tujuan Pembelajaran
Dengan membaca bahan ajar, berdiskusi, dan menggali informasi di berbagai sumber, peserta didik dapat memahami materi ajar dan mengembangkan kompetensi diri dalam penerapan kehidupan sehari-hari dengan tepat
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
Untuk lebih jelasnya simak dan pahami materi ajar berikut ini!
Selain membaca bahan ajar di blog ini, kalian juga bisa membaca di buku paket matematika dan menggali informasi dari berbagai sumber.
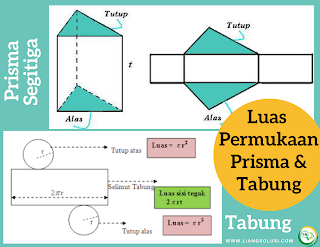
Luas Permukaan Prisma dan Tabung
Baca juga materi tentang:
Luas Permukaan Prisma dan Tabung
1. Prisma
Prisma merupakan salah satu jenis bangun ruang yang dibatasi oleh sisi alas dan sisi tutup serta sisi-sisi tegak yang berbentuk persegi atau persegi panjang.
Penamaan prisma tersebut berdasarkan bentuk alas dan tutupnya. Alas dan tutup prisma memiliki bentuk dan ukuran yang sama (kongruen).
Karakteristik prisma segi-n yaitu sebagai barikut.
- Prisma memiliki n + 2 sisi. 2 sisi yaitu sisi alas dan sisi tutup serta n sisi tegak.
- Banyaknya titik sudut pada prisma adalah 2n.
- Prisma memiliki 3n rusuk, n rusuk pada sisi alas, n rusuk pada sisi tutup, dan n rusuk pada sisi tegak.
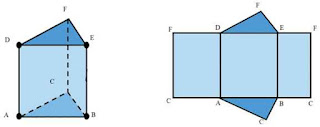
Perhatikan jaring-jaring dan ukuran prisma segitiga berikut.
L = L ABC + L DEF + L FDAC + L DEBA + L EFCB L = (2 x L ABC) + [(CA x AD) + (AB x BE) + (BC x CF)
L = (2 x L ABC) + [(CA + AB + BC) x AD]
L = (2 x La) + (K ABC x AD)
L = (2 x La) + (Ka x t)
Keterangan:
L = (2 x La) + (K ABC x AD)
L = (2 x La) + (Ka x t)
Keterangan:
L adalah luas permukaan prisma
La adalah luas alas prisma
K adalah panjang keliling
Ka adalah panjang keliling alas prisma
t adalah tinggi prisma
Karena alas dan tutup prisma memiliki bentuk dan ukuran yang sama, maka keduanya memiliki luas yang sama juga, sehingga
Luas permukaan prisma = 2 x luas alas + luas sisi-sisi tegak
Jika kita lihat sisi-sisi tegak (selimut prisma) dalam jaring-jaring di atas berbentuk persegi panjang, dengan panjangnya merupakan keliling alas prisma dan lebarnya merupakan tinggi prisma.
Lp = (2 x L alas) + (K alas x t)
Keterangan:
Lp : luas permukaan prisma
L alas : luas alas prisma
K alas : keliling alas prisma
t : tinggi prisma
Luas permukaan tabung dapat dihitung dengan menjumlahkan luas ketiga sisinya, yaitu
Luas Permukaan Tabung = Luas Alas + Luas Atap + Luas Selimut Tabung
Luas alas = luas atap = π × r²
Luas selimut tabung = 2 × π × r × t
Jadi Luas Permukaan tabung adalah
L = π × r² + π × r² + 2 × π × r × t
L = 2 × π × r² + 2 × π × r × t
L = 2 π r (r + t)
Keterangan :
L = Luas permukaan tabung
π = phi (22/7 atau 3,14)
r = jari – jari alas / atap
t = tinggi tabung
La adalah luas alas prisma
K adalah panjang keliling
Ka adalah panjang keliling alas prisma
t adalah tinggi prisma
Luas permukaan prisma = luas alas + luas tutup + luas sisi-sisi tegak
Karena alas dan tutup prisma memiliki bentuk dan ukuran yang sama, maka keduanya memiliki luas yang sama juga, sehingga
Luas permukaan prisma = 2 x luas alas + luas sisi-sisi tegak
Jika kita lihat sisi-sisi tegak (selimut prisma) dalam jaring-jaring di atas berbentuk persegi panjang, dengan panjangnya merupakan keliling alas prisma dan lebarnya merupakan tinggi prisma.
Lp = (2 x L alas) + (K alas x t)
Keterangan:
Lp : luas permukaan prisma
L alas : luas alas prisma
K alas : keliling alas prisma
t : tinggi prisma
Contoh:
1. Sebuah prisma alasnya berbentuk segitiga siku siku dengan panjang alas 20 cm, tinggi 15 cm, dan tinggi prisma 25 cm. Tentukan luas permukaannya!
Penyelesaian
Diketahui p.alas = 20 cm, t.segitiga = 15 cm, t.prisma = 25 cm
Ditanyakan luas permukaan prisma?
L = (2 x luas segitiga) + (keliling alas×tinggi prisma)
Karena alasnya berbentuk segitiga siku-siku, untuk menghitung luasnya, maka kita harus mengetahui sisi miring segitiga dengan rumus Pythagoras.
a² + b² = c²
15² + 20² = c²
625 = c²
c = 25 cm
L = (2 x luas segitiga) + (keliling alas×tinggi prisma)
L = (2 x ½ x 20 x 15) + {(20 + 15 + 25) x 25}
L = 300 cm² + 1.500 cm²
L = 1.800 cm²
Jadi, luas permukaan prisma tersebut 1.800 cm²
2. Sebuah prisma, alasnya berbentuk segitiga siku-siku. Jika tinggi segitiga 16 cm, panjang alas 30 cm, dan tinggi prisma 18 cm. Berapa luas permukaannya?
Penyelesaian
Diketahui p.alas = 30 cm, t.segitiga = 16 cm, t.prisma = 18 cm
Ditanyakan luas permukaan prisma?
L = (2 x luas segitiga) + (keliling alas×tinggi prisma)
Karena alasnya berbentuk segitiga siku-siku, untuk menghitung luasnya, maka kita harus mengetahui sisi miring segitiga dengan rumus Pythagoras.
a² + b² = c²
16² + 30² = c²
1.156 = c²
c = 34 cm
L = (2 x luas segitiga) + (keliling alas x tinggi prisma)
L = (2 x ½ x 30 x 16) + {(30 + 16 + 34) x 18}
L = 480 cm² + 1.440 cm²
L = 1.920 cm²
Jadi, luas permukaan prisma tersebut 1.920 cm²
2. Tabung
Tabung adalah salah satu bangun ruang sisi lengkung. Secara spesifik, tabung adalah suatu bangun ruang berbentuk prisma tegak beraturan dengan alas dan tutupnya berupa lingkaran.
Sifat-sifat Tabung
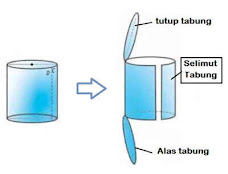
- Mempunyai 3 bidang sisi : alas, tutup dan selimut (sisi tegak)
- Bidang alas dan tutup berupa lingkaran
- Sisi tegak berupa bidang lengkung yang dinamakan selimut tabung
- Mempunyai 2 rusuk : rusuk alas dan tutup
- Tinggi tabung: jarak titik pusat alas dan titik pusat tutup
- Jari-jari lingkaran alas dan tutup besarnya sama
Luas Permukaan Tabung = Luas Alas + Luas Atap + Luas Selimut Tabung
Luas alas = luas atap = π × r²
Luas selimut tabung = 2 × π × r × t
Jadi Luas Permukaan tabung adalah
L = π × r² + π × r² + 2 × π × r × t
L = 2 × π × r² + 2 × π × r × t
L = 2 π r (r + t)
Keterangan :
L = Luas permukaan tabung
π = phi (22/7 atau 3,14)
r = jari – jari alas / atap
t = tinggi tabung
Contoh
1. Sebuah toples berbentuk tabung dengan diameter 14 cm dan tingginya 10 cm. Luas seluruh permukaanya adalah .... (π= 22/7)
Penyelesaian
Diketahui d = 15 cm, r = 7,5 cm, dan t = 10 cm
Ditanyakan luas permukaan tabung?
Luas seluruh permukaan tabung = 2 πr x (r + t)
Luas seluruh permukaan tabung = 2 (22/7 x 7 cm) x (7 cm + 10 cm)
Luas seluruh permukaan tabung = 748 cm²
2. Putu Indra akan menghias kaleng berbentuk tabung tanpa tutup dengan luas selimut 880 cm². Jika diketahui tinggi kaleng 10 cm, Berapakah kain yang dibutuhkan Putu Indra untuk melapisi kaleng tersebut?
Penyelesaian
Diketahui luas selimut tanpa tutup = 880 cm², t = 10 cm
Ditanyakan luas permukaan tabung?
Untuk menghitung luas permukaan tabung, kita harus mengetahui r nya
Luas selimut tabung = 880 cm²
2 x π x r x t = 880 cm²
2 × 22/7 × r × 10 = 880 cm²
440/7 r = 880 cm²
r = 880 cm² : 440/7 = 880 cm² x 7/440
r = 14 cm
Luas permukaan tabung tanpa tutup = luas selimut + luas alas
Luas permukaan tabung tanpa tutup = 880 cm² + (π x r²)
Luas permukaan tabung tanpa tutup = 880 cm² + (22/7 x 14²)
Luas permukaan tabung tanpa tutup = 1.496 cm²
Kolaborasi dan Praktik Baik
Kerjakan pertanyaan berikut untuk meningkatkan keterampilan dan mengembangkan kompetensi numerasimu dalam penerapan kehidupan sehari-hari (Kerjakan di buku latihanmu dengan menyertai tanda tangan orang tua!)
- Pak Made Suta memiliki drum minyak tanah berbentuk tabung. Diameter tangki tersebut 140 cm dan tingginya 2 meter. Agar tidak berkarat, tangki tersebut akan dicat. Tiap m² menghabiskan biaya sebesar Rp20.000,00 lebih murah Rp5.000,00 dari biasanya. Berapa biaya yang harus dikeluarkan Pak Made Suta untuk mengecat drum tersebut?
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
Bagaimana kegiatanya, menyenangkan bukan? Pekerjaan kalian yang sudah bagus dan luar biasa akan jauh lebih bermanfaat jika dilakukan presentasi atau di diskusikan dengan teman, orang tua, dan guru kalian. Hal ini bertujuan untuk meningkatkan rasa percaya diri dan membangun pengetahuan baru.
Hasil diskusi dan presentasi yang sudah kalian lakukan dapat dijadikan sebagai motivasi diri untuk perbaikan pembelajaran yang akan datang. Masukan atau saran juga kritik yang membangun dapat membangun karakter dan pengetahuan diri yang lebih baik.
Nah, untuk mengetahui pemahaman pembelajaran yang sudah kalian simak dan lakukan, ada baiknya juga kalian melakukan refleksi atau merangkum kegiatan pembelajaran hari ini. Hal tersebut bertujuan untuk menguji pemahaman kompetensi diri terhadap pembelajaran daring yang kalian lakukan secara mandiri dari rumah. Refleksi ini dapat dilakukan dengan menjawab pertanyaan singkat. Seperti :
Apa yang sudah saya pelajari hari ini?
Dapatkah saya menguasai materi pembelajaran hari ini?
Apa Manfaat yang saya dapatkan dengan mempelajari materi tersebut?
Demikian tayangan materi singkat Pembelajaran Jarak Jauh Matematika Tentang Luas Permukaan Prisma dan Tabung untuk Kelas 6 SD. Untuk menguji pemahaman dan penguasaan kompetensi pembelajaran hari ini, lakukanlah kegiatan formatif berikut ini dengan menjawab soal yang terdiri dari 10 butir soal pilihan ganda dalam bentuk aplikasi google form.
Baca dan ikuti petunjuk soal yang disediakan. Jawab soal berikut dengan cermat agar bisa mengukur capaian kompetensi yang dimiliki.
Waktu pengerjaan dari Liang Solusi: 120:00 Menit!
Klik Saja untuk kalian yang ingin mengembangkan kompetensi melalui materi, penugasan dan penilaian soal formatif pada setiap pembelajaran
Setelah menyelesaikan soal tersebut, lihatlah skor perolehan kalian dan skor perolehan teman-teman kalian dari sekolah maupun antar sekolah pada form berikut ini!
Terima kasih sudah menyimak materi dan mengerjakan Pembelajaran Matematika Tentang Luas Permukaan Prisma dan Tabung untuk Kelas 6 SD. Isi postingan ini tentu belum lengkap dan memberikan pembelajaran bermakna.
Untuk itu, kritik dan saran sangat dibutuhkan untuk meningkatkan kualitas situs www.liangsolusi.com ini. Semoga materi dan evaluasi formatif yang dilakukan bermanfaat untuk kalian. Salam solusi!
Kami sangat berterima kasih jika pembelajar berkenan membagikan postingan ini di media sosial! Budayakan meninggalkan komentar dan sebarkan jika bermanfaat setelah mengerjakannya. Semoga bertambah cerdas dan berkarakter.
#MerdekaBelajar
#CerdasBerkarakter
#Belajardarimanasaja











0 comments:
Posting Komentar